貨幣需要の在庫理論アプローチとは、貨幣範囲を現金通貨に限定し、取引動機に基づく貨幣保有による便益と機会費用から、最適な貨幣保有残高を分析したものであり、ボーモル・トービン（Baumol-Tobin）モデルとも呼ばれる。貨幣保有を増大させると、その分を銀行預金や債券として保有した場合に受け取ることができたであろう金利収入である機会費用が増大する。一方、貨幣保有を増大させると、預金を引き出す回数が減少するため、取引費用を削減できる。例えば、銀行預金を一度に全て引き出すならば、預金残高に応じて得られる金利収入は得られないが、手数料や銀行に出向くための費用（shoe leather costs）である取引費用を削減できる。この取引費用の削減分が、貨幣保有の便益である。一方、その都度消費に必要な現金のみを引き出して預金残高を保てば、金利収入を得られるが、取引費用が増加する。こうした貨幣保有による機会費用と取引費用を合わせた費用が最小化される預金引き出し回数における平均貨幣保有残高が最適な貨幣保有残高となる。

設定

　今、初期時点においてY円の所得（例えば、1か月あたりの収入がY円）を銀行預金として保有する家計が、時間を通じて一定の消費水準を保つために、一定期間（先の例では1か月）にY円をN回に分けて預金口座から引き出し、その際に1回あたりf円の取引費用が発生するものとする（期末にN回目の引き出しを行い、預金残高がゼロとなる）。一方、預金者は預金残高に応じて金利iを受け取ることができるものとする。家計は金利収入と取引費用の差である収入を最大化するように引き出し回数Nを決定するものとする。

解説

　以上の想定の下で、一定期間内にN回の預金引き出しを行う場合、貨幣残高も推移は図1のように表せる。

　図より、平均貨幣保有残高は円であり、貨幣保有によって放棄しなければならない金利収入（貨幣保有の機会費用）は円となる。一方、預金引き出しにかかる取引費用はfN円である。したがって総費用Cは、

(1)

と表される。このとき、総費用を最小化する最適預金引き出し回数N*は、

より、

(2)

となる。(2)式を平均貨幣保有残高に代入すると、最適な平均貨幣保有残高は、

平均保有残高 (3)

となる。

　上式より、在庫理論アプローチにおける貨幣需要は、所得Y、金利i、および、取引コストfに依存し、所得Yが増加したとき、金利iが低下したとき、および、取引コストfが増大したとき、増加することがわかる。

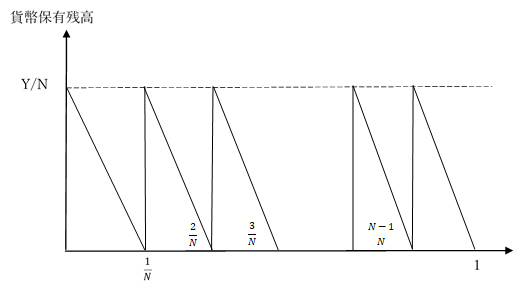
図1.1か月間を通じた貨幣保有残高の推移

参考文献

Baumol, W. J. (1952). “The Transactions Demand for Cash: An Inventory Theoretic Approach”. Quarterly Journal of Economics. 66 (4): 545–556. 

Baumol, W.J. and Tobin, J. (1989). “The Optimal Cash Balance Proposition: Maurice Allais’ Priority”. Journal of Economic Literature. 27 (3): 1160–1162.

Tobin, J. (1956). “The Interest Elasticity of the Transactions Demand for Cash”. Review of Economics and Statistics. 38 (3): 241–247. 

文責：経営管理研究科　後藤瑞貴

本ウェブサイトは、一橋大学大学院経営管理研究科とみずほ証券の共同研究の成果を、一橋大学大学院経営管理研究科が用語集（学術）にまとめ、掲載したものです。本ウェブサイトは、金融論・ファイナンス理論の分野で注目されている研究テーマや主要な先行研究に関心をお持ちの方の学習・研究の一助となることを専らの目的としています。本ウェブサイトは、一橋大学大学院経営管理研究科が運営しています。なお、各用語集（学術）の著作権は各執筆者に帰属します。